MULTIMI FUZZY
Laborator TICE 27.02.2008/Gbr
Contents
Fiecare echipa de lucru va crea un director cu nume sugestiv in care va salva toate rezultatele obtinute la rezolvarea exercitiilor si anume scripturi matlab si un fisier word ce va include toate rezultatele numerice si cele grafice.
OBIECTIVE
- Ilustrarea vizuala a conceptului de multime fuzzy (mf)
- Familiarizarea cu tipurile de mf implementate in Fuzzy Logic Toolbox din Matlab
- Intelegerea operatiilor cu mf (complement, reuniune, intersectie)
- Familiarizarea cu editorul de multimi fuzzy "mfedit"
GALERIA DE MULTIMI FUZZY
Pentru a vizualiza in Matlab tipurile de mf diponibile in fereastra de comenzi se scrie:
close all; % inchide toate ferestrele mfdemo;
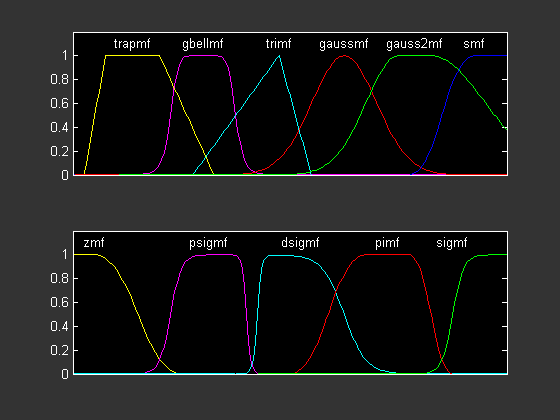
UTILIZAREA MULTIMILOR FUZZY IN MATLAB
Pentru a afla detalii despre fiecare din cele 11 mf se scrie: 'help nume_multime' De exemplu pentru "trapmf":
help trapmf
TRAPMF Trapezoidal membership function.
TRAPMF(X, PARAMS) returns a matrix which is the trapezoidal
membership function evaluated at X. PARAMS = [A B C D] is a 4-element
vector that determines the break points of this membership function.
We require that A <= B and C <= D. If B >= C, this membership
function becomes a triangular membership function that could have
a height less than unity. (See the example below.)
For example:
x = (0:0.1:10)';
y1 = trapmf(x, [2 3 7 9]);
y2 = trapmf(x, [3 4 6 8]);
y3 = trapmf(x, [4 5 5 7]);
y4 = trapmf(x, [5 6 4 6]);
plot(x, [y1 y2 y3 y4]);
set(gcf, 'name', 'trapmf', 'numbertitle', 'off');
See also DSIGMF, EVALMF, GAUSS2MF, GAUSSMF, GBELLMF, MF2MF, PIMF, PSIGMF,
SIGMF, SMF, TRIMF, ZMF.
Reference page in Help browser
doc trapmf
Rulati secventa urmatoare
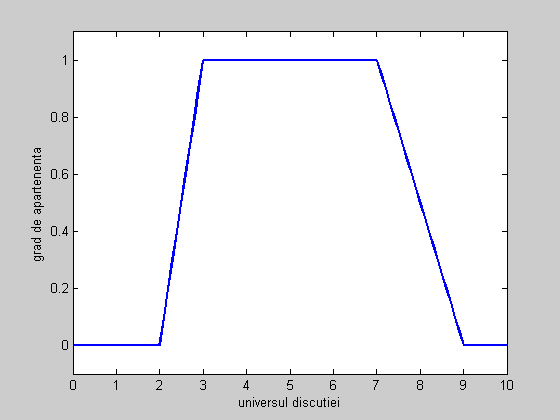
close all % inchide figura anterioara clear all % sterge toate variabilele existente in workspace clc % sterge consola (fereastra de comenzi) x = (0:0.1:10)'; % Universul discutiei este [0,10], in care se definesc puncte cu pasul de 0.1 params=[2 3 7 9];% parametrii multimii fuzzy trapezoidale y = trapmf(x,params); % calculeaza valorile functiei de apartenenta plot(x, y,'linewidth',2); axis([0 10 -0.1 1.1]); xlabel('universul discutiei'); % numele variabilei pe axa orizontala ylabel ('grad de apartenenta'); % numnele variabilei pe axa verticala set(gcf, 'name', 'Multime fuzzy trapezoidala', 'numbertitle', 'off'); % numele ferestrei
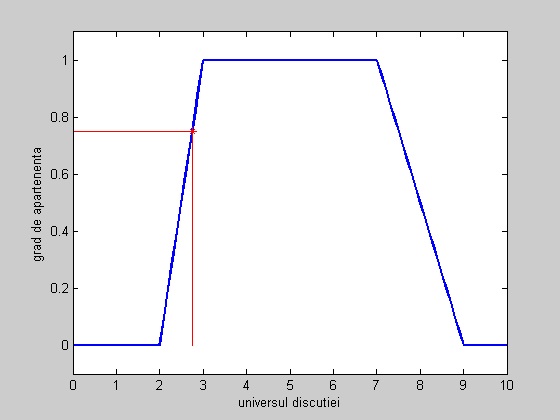
Determinarea gradului de apartenenta. Rulati secventa urmatoare pentru a afla gradul de apartenenta al punctului x1=2.75, la mf trapezoidala.
hold on x1=2.75; u1=evalmf(x1,params,'trapmf'); sprintf('Valoarea x1=%1.2f are gradul de apartenenta u1=%1.2f',x1,u1); plot (x1,u1,'r*') % marcheaza punctul pe grafic plot ([x1,x1],[0,u1],... 'linestyle','-','color','r') plot ([0,x1],[u1,u1],... 'linestyle','-','color','r') hold off
Exercitii
- 1. Reprezentati grafic alte doua tipuri de multimi fuzzy la alegere, considerand universul discutiei [-5, 8].
- 2. Scrieti un script matlab pentru rezolvarea acestui exercitiu. Considerati variabila lingvistica "Viteza", cu universul discutiei [0,140]km/h. Definiti trei valori lingvistice si reprezentati grafic cele trei mf corespunzatoare, pe aceasi axa (folositi "hold on"), fiecare cu alta culoare. Care sunt gradele de apartenenta la fiecare multime a valorilor vitezei de 10km/h, 52km/h, 85 km/h si 100km/h?
OPERATII CU MULTIMI FUZZY
Reuniunea a doua multimi fuzzy A si B o definim cu ajutorul functiilor de apartenenta:
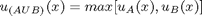
Reprezentarea grafica a reuniuni a doua multimi.
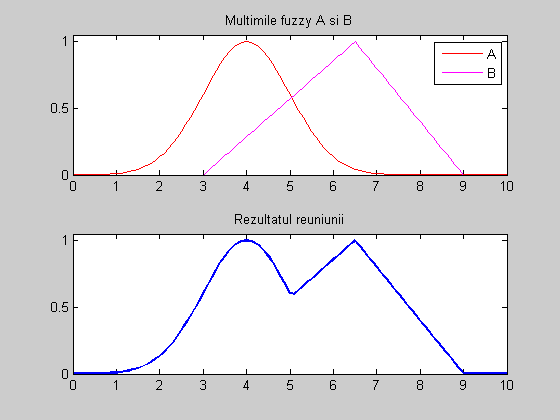
Rulati secventa urmatoare pentru a reprezenta grafic rezultatul reuniunii a doua multimi fuzzy.
close all x = (0:0.1:10)'; % Universul discutiei este [0,10], in care se definesc puncte cu pasul de 0.1 u1=gaussmf(x,[1,4]); % prima mf, gaussiana u2=trimf(x,[3 6.5 9]); % a doua mf, triunghiulara u_reuniune=max(u1,u2); % calculeaza gradele de aparteneta ale reuniunii prin operatorul "MAX" hold on subplot(2,1,1); % imparte fereastra de reprezentare a unei figuri in doua regiunii verticale % graficul se afiseaza in fereastra de sus plot (x,u1,'r');hold on plot (x,u2,'m'); hold off axis([0 10 0 1.05]); legend ('A','B'); title('Multimile fuzzy A si B') subplot (2,1,2) % se va afisa in fereastra de jos plot(x, u_reuniune,'color','b','linewidth',2) axis([0 10 0 1.05]); title('Rezultatul reuniunii') set(gcf, 'name', 'Reuniunea multimilor fuzzy A si B - operatorul "max"', 'numbertitle', 'off'); % numele ferestrei
Exercitii
- 1. Scrieti un script matlab pentru reprezentarea grafica a rezultatului operatiei de intersectie a multimilor fuzzy A si B, utilizand operatorul "min". Utilizand "Data Cursor" din bara de instrumente marcati pe grafic gradele de apartenenta pentru valorile x=4,5,6,7.
- 2. Scrieti un script matlab pentru reprezentarea grafica a rezultatului operatiei de complementare a multimii fuzzy A utilizand operatia:
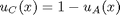
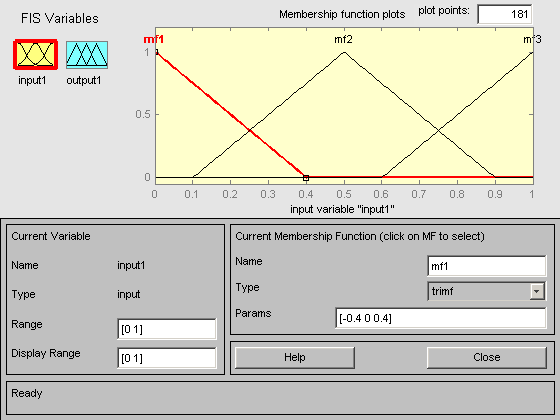
EDITORUL DE MULTIMI FUZZY "mfedit"
Lansati in executie editorul grafic de multimi fuzzy cu comanda "mfedit".
close all
mfedit
Exercitiu
- Considerati variabila lingvistica "Viteza", cu universul discutiei [0,140]km/h. Definiti cinci valori lingvistice si construiti mf corespunzatoare. Folositi urmatoarele tipuri de multimi fuzzy: 'zmf', 'gbellmf' si 'smf'.